Quantum Computing
Classical Data Structures for Representing Quantum Information with High Entanglement
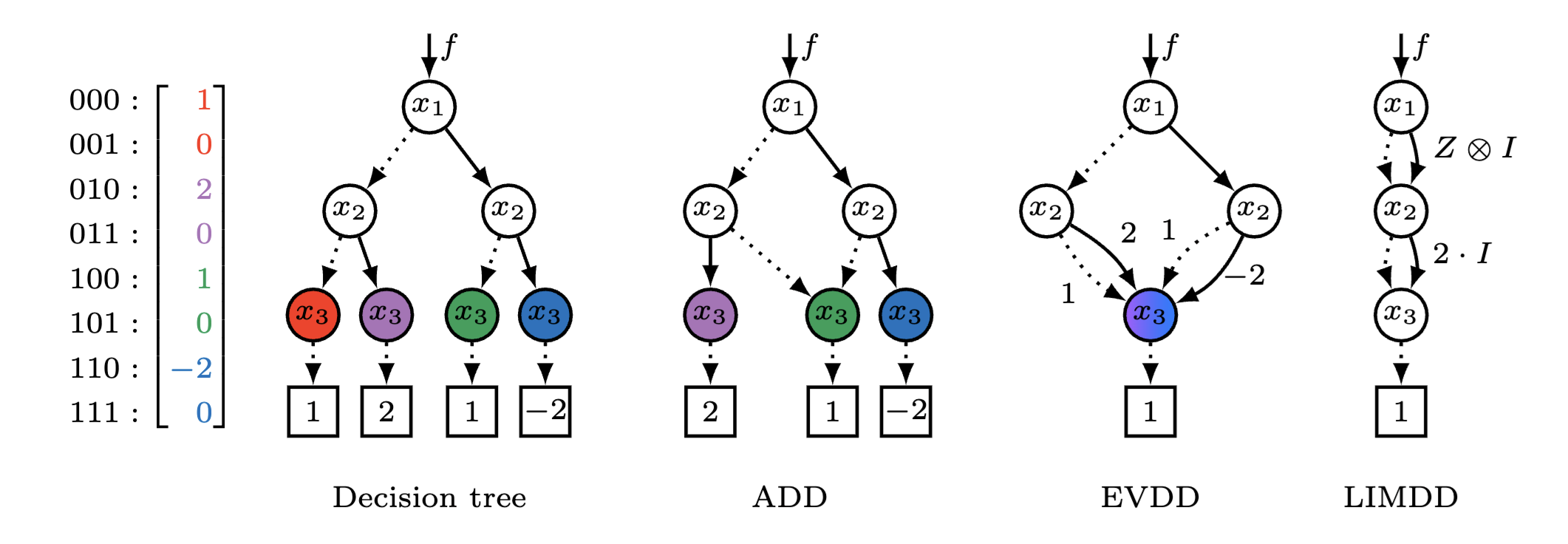
LIMDD: My team proved that decision diagrams (DDs), which were used to represent and manipulate quantum states, cannot efficiently represent high-entanglement structures. Concretely, we found that for certain (families of) stabilizer states, the diagram grows exponentially large. The resolve this bottleneck, we proposed the Local Invertible Map Decision Diagram (LIMDD). LIMDD can be viewed as a non-trivial combination of Gottesman and Aaronson's stabilizer formalism and the decision diagram: It allows merging of DD nodes representing quantum states that are equivalent up to "destabilizers" (previous DD variants only merge nodes representing states that are equivalent up to a constant factor). We can show that, while previous DDs are strictly less expressive than certain tensor networks (MPS or tensor trains), the LIMDD can be exponentially more expressive than these tensor networks. We also show that classical simulation of quantum circuits with LIMDD can be exponentially faster than with certain stabilizer rank-based methods.
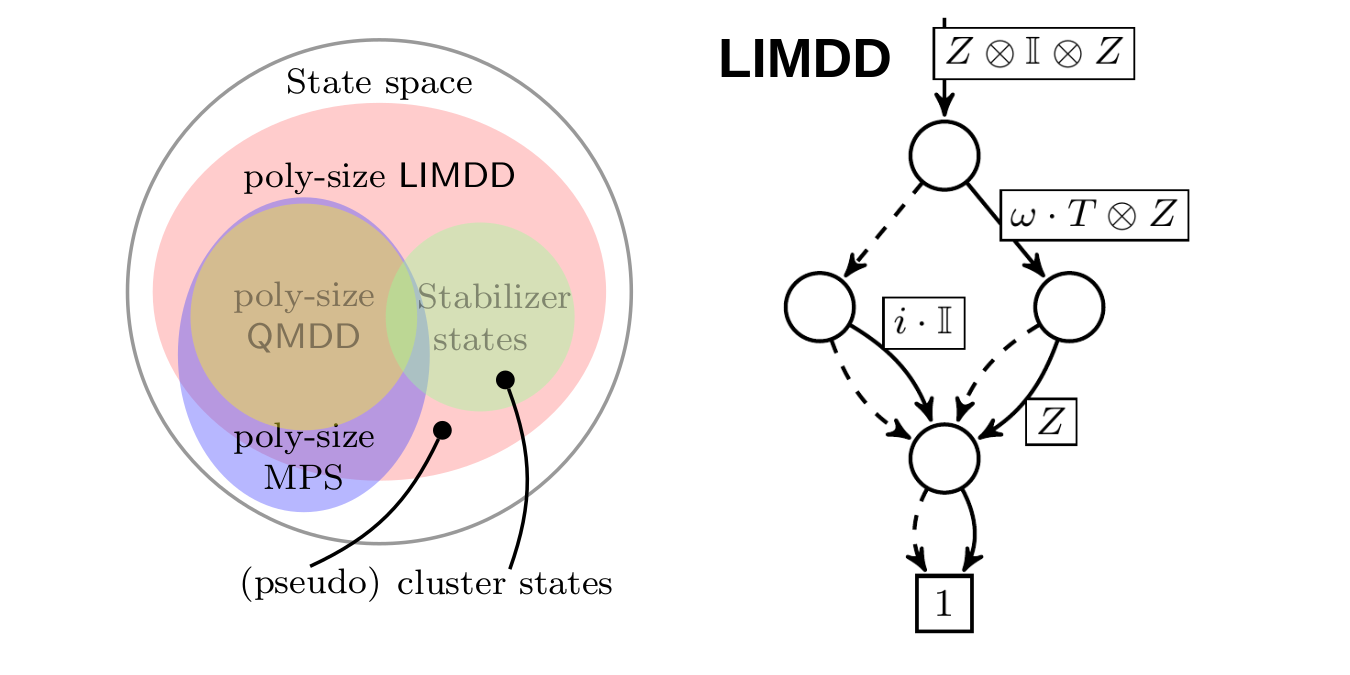
A Knowledge Compilation Map for Quantum Information: Darwiche and Marquis proposed the knowledge representation map for analytically comparing data structures representing Boolean functions. The map charts relative succinctness (or expressivity) of data structures by identifying families of functions that are exponential in one representation but polynomial in the other. Moreover, it also maps the tractability of performing different operations on these data structures (e.g., conjoining two functions, model counting, satisfiability, etc), showing, as expected, that succinctness typically sacrifices tractability.
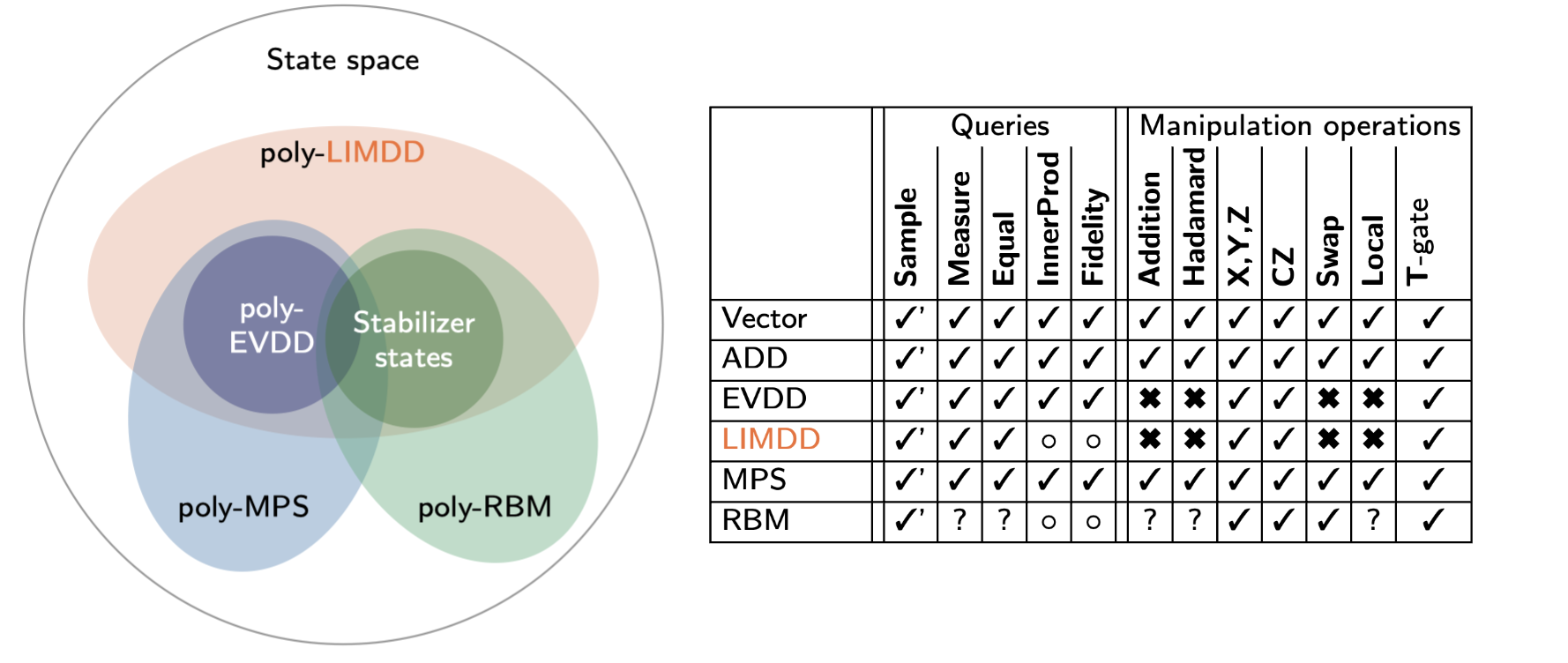
We give the first knowledge compilation map for quantum information, focusing on the following data structures: (Edge-Valued) Decision Diagram, Tensor Network (in particular, Matrix Product State, MPS, or tensor trains) and Quantum Neural Networks (in particular, the Restricted Boltzmann Machine, RMB). We study the tractability of quantum operations relevant to quantum circuit simulation and equivalence checking, and variational quantum algorithms. Our study shows several surprising results:
- Tensor Trains is exponentially more succinct (expressive) than Decision Diagrams.
- LIMDD, Tensor Trains and RBM are incomparable in terms of succinctness, i.e., there is an exponential succinctness separation in all directions; a family of states that is small in the one but exponentially large in the other data structure.
- Under standard complexity-theoretic assumptions, computing fidelity and inner product is hard for any data structure that can succinctly represent graph states and Dicke states. This includes both LIMDD and RBM.
- Decision Diagrams can be polynomially simulated by MPS.
The last result above was established by extending the notion of rapidity by Lai, Liu & Yin (2017), which resolves an important shortcoming of the compilation map: Tractability alone often suggests that a data structure is efficient merely because it never succinct. For instance, a plain state vector representation allows many hard queries in time linear in its size, simply because it is an exponential object. Rapidity remedies this by comparing the tractability of operations on one data structure, taking the size of another data structure as a unit. This for instance reveals that Edge-Valued DDs polynomially simulate certain operations in Multi-Terminal DDs, despite the fact that the former is intractable and the latter is tractable. We extended the notion of rapidity with support for non-canonical data structures and provide simple sufficient conditions for showing that a data structure is as rapid as another.
Bottom line: Our results reveal important bottlenecks in existing data structures used ubiquitously for simulating and analyzing quantum systems. We resolve some of these issues with LIMDD, while at the same time opening up a new toolbox for analyzing other possible combinations and extensions. LIMDD has been implemented (see LIMDD-sim), and extended by the group of Mingshen Ying.
Hybrid Quantum Computing
Divide & Quantum: We studied the preservation of quantum speedups under classical parallelization. Viewed alternatively, we asked the question how large a problem can be solved with a small quantum computer while preserving its speedup. The strategy here is to classically split the problem (divide) until it is small enough to be solved on the quantum computer with few qubits. Here, we define few as a constant fraction of the original problem size, since we strive to demonstrate "threshold-free" preservation of speedups. Focusing on Montanaro's Quantum Tree Search, we provide sufficient conditions for the preservation of threshold-free speedups. We provide a space-efficient implementation of Montanaro's "Quantum DPLL" to realize these conditions. In addition, we show how the Grover algorithm can be combined with PPSZ to realize a best worst-case quantum satisfiability algorithm which also preserves threshold-free speedups in the Divide & Quantum setting.
Space-efficient Quantum Computing
Tradeoffs between Classical and Quantum Space: Since our Divide & Quantum algorithms hinge on space-efficient algorithms, we studied time and space tradeoffs in dynamic quantum circuits. Dynamic quantum circuits allow measurement-based uncomputing, which effectively replaces quantum space with classical space. The space complexity of these circuits can be studied using the Spooky pebble game introduced by Craig Gidney. We show that finding an optimal spooky pebbling of a circuit is PSPACE complete. We also develop a combination of heuristic simplification strategies and SAT solver encodings to solve the pebble game in practice. The basic approach is reminiscent of Bounded Model Checking, with an additional loops to optimize over the number of pebbles used.
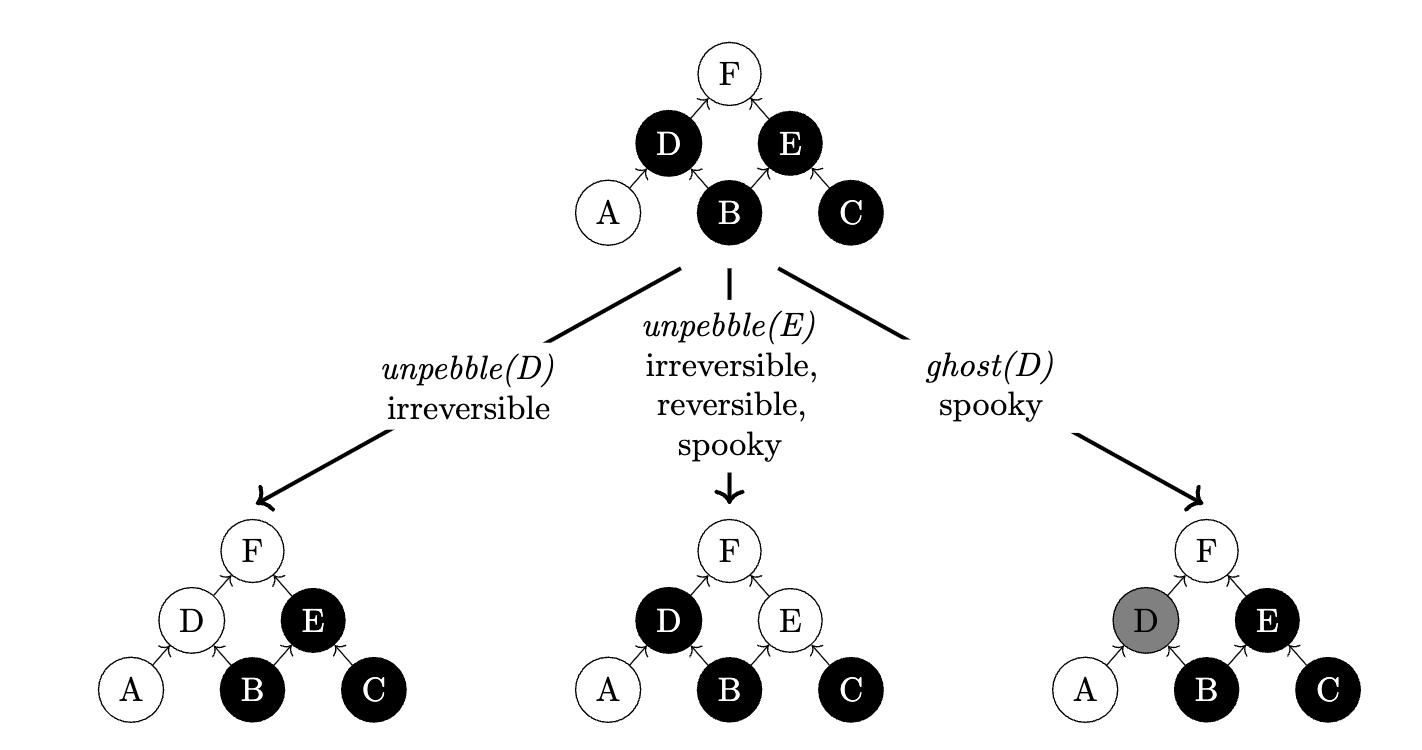
Bottom line: Divide & Quantum enables the use of small quantum computers for larger problems while preserving speedups. Our threshold-free speedup theorem reveals the importance of having space-efficient quantum algorithm implementation in this setting. For this reason, we studied spooky pebbling. Our PSPACE-completeness result was further extended by Kornerup, Sadun and Soloveichik.
Reducing Quantum Computing to #SAT
Quantum Circuit Simulation through Weighted Model Counting: We reduced quantum circuit simulation to weighted model counting, or #SAT.

Quantum Computing and Automated Reasoning
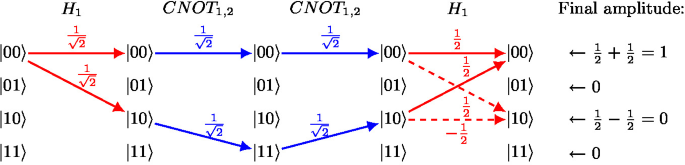
Advancing Quantum Computing with Formal Methods: This tutorial explains quantum computing for a formal methods audience. Quantum computing is positioned as a natural extension of both probabilistic and reversible computing. We build on the intuition of probabilistic system analysis to explain the basics of quantum circuit semantics. The tutorial also connects reduces problems in quantum computing to the tools available in the formal methods toolbox. Quantum circuit simulation is reduced to #SAT, providing insight into circuit semantics through the logic formulation. Similarly, many examples show how simulation and equivalence checking can be done with decision diagrams.
Automated Reasoning in Quantum Circuit Compilation: We present a comprehensive survey of how classical automated reasoning techniques ---such as decision diagrams, SAT solving, and graphical calculi--- are being systematically adapted to address the complex challenges inherent in quantum circuit compilation. Despite the fundamentally quantum nature of the problem domain, many hard tasks like circuit equivalence checking, synthesis, and optimization can be effectively reformulated into classical reasoning frameworks, particularly through weighted model counting (#SAT) and advanced decision diagram representations like EVDDs, CFLOBDDs, and LIMDDs. Decision diagrams offer compact, scalable representations of quantum states, enabling efficient simulation and symbolic verification, while SAT-based methods can encode synthesis and optimization constraints, allowing the use of mature, high-performance classical solvers for quantum compilation problems. Additionally, graphical calculi like ZX-calculus provide a complementary, visual framework for equational reasoning and circuit rewriting, enhancing the ability to formally verify and optimize quantum circuits. We illustrate how these techniques, though stemming from classical formal verification and logic synthesis, can be combined into robust toolchains that rival or surpass specialized quantum-native tools in scalability and correctness guarantees.
Parallel Computing
Parallel Depth-First Search
A classical result by Reif shows that depth-first search (DFS) is likely not parallelizable. We show nonetheless that parallel processes, exploring the graph with randomized and communicating DFSs, can preserve enough of the original DFS order to be useful for solving important problems such as cycle identification, Büchi emptiness checking, and SCC detection.
Parallel Nested Depth-First Search: To solve Büchi emptiness checking, we investigated new parallel versions of nested depth-first search. We let processes explore the graph initially independently and share information in the backtrack so that they prune each others search space. While in the worst case this approach yields no speedup, we find that for many large graphs arising in model checking the approaches scales well in practice.
In parallel with our work, Evangelista, Petrucci, and Youcef came up with an orthogonal approach which lets processes also communicate in the forward search. Both works were published at ATVA 2011. Our teams joint forces to integrate these approaches in one new algorithm called CNDFS.

Parallel On-The-Fly SCC Algorithm: Based on the new parallelization techniques that we developed for depth-first search algorithms, we presented a novel parallel, on-the-fly SCC algorithm. It preserves the linear-time property by letting workers explore the graph randomly while carefully communicating partially completed SCCs. We prove that this strategy is correct despite the more lenient DFS orders that it allows. For efficiently communicating partial SCCs, we develop a concurrent, iterable disjoint set structure, combining the union-find data structure with a cyclic list. Jayanti and Tarjan later derived a new line of data structure to support our algorithm. Based on our results, Lowe later formulated a parallel SCC algorithm that ensures more parallelism by synchronizing on the stack data structure.
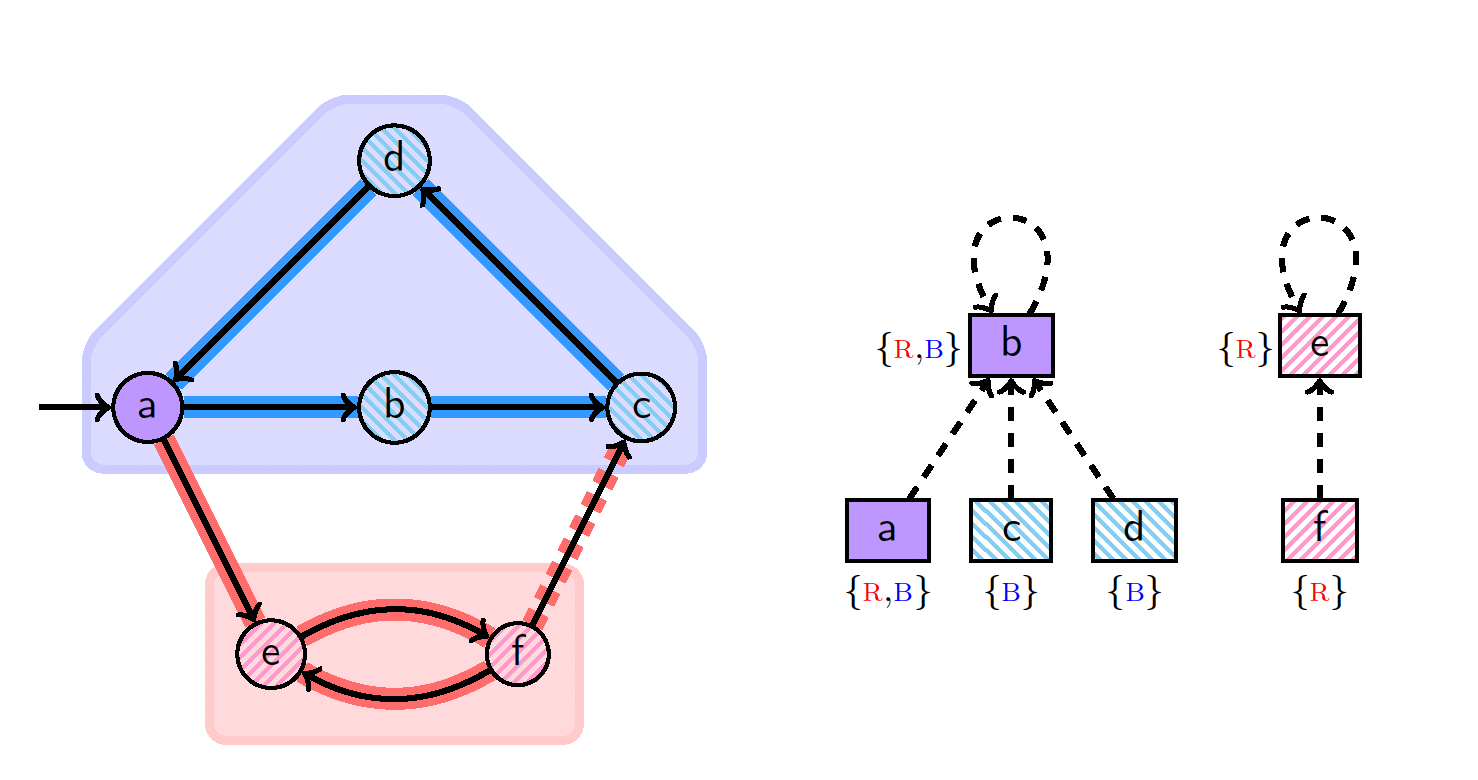
Parallel Feedback Sets: A vertex feedback set is a set of edges covering all cycles in a graph. We showed that our parallel DFS strategy can also be leveraged to find good feedback sets.